PIERRE SIMÒN LAPLACE
Nace el 28 de marzo de 1749 en Beaumont en Auge Normandia, Francia; fuè astrònomo, fisìco y matemàtico frànces que invento y desarrollo la transformada de Laplace y la ecuación de Laplace. Compartió la doctrina Filosofica del determinismo cientifíco.
Estudió en la Universidad de D'Alembert, quien impresionado por su habilidad matemática, lo recomendo para un puesto de profesor en la Escuela Militar de París, en 1767, donde tuvo entre discípulos a Napoleón. En 1785 es nombrado miembro de la Academia de Ciencia y en 1795, miembro de la cátedra de matemática del Nuevo Instituto de las Ciencias y las Artes, que presidirá en 1812. En 1788 se casó con la joven Marie Charlotte de Country de Romanges, perteneciente a una familia de Besancon, 20 años mas joven que él, con quien tuvo dos hijos Sophie Suzanne y Charles Emile, nacido en 1789 y él alcanzaría el grado de general. En 1795, Laplace empezó a publicar el primero de cinco volúmenes que constituirían su Mecanica Celeste y en 1796 imprime su Exposition du systeme du monde, donde revela su hipótesis nebular sobre la formación del sistema solar. En 1799, fue nombrado ministro del interior durante el Consulado, estuvo seis semanas en el cargo. En 1805, su antiguo alumno Napoleón le confirio la legión de honor. En 1806, el t´titulo de conde del Imperio. En 1812 pública su Teoría Analítica de las Probabilidades. En 1814 su Ensayo filosofico sobre Probabilidad. En 1816, fue elegido miembro de la Academia Francesa.
Sentó las bases científicas de la teoría matemática de probabilidades (en su obra Théorie Analytique desprobabilites, donde entre otros logros formuló el método de los minimos cuadrados que es fundamental para la teoría de errores) y formuló de manera muy firme e influyente la imagen de un mundo completamente determinante.
"Podemos mirar el estado presente del universo como el efecto del pasado y la causa de su futuro. Se podría concebir un intelecto que en cualquier momento dado conociera todas las fuerzas que animan la naturaleza y las posiciones de los seres que la componen; si este intelecto fuera lo suficientemente vasto como para someter los datos a análisis, podría condensar en una simple fórmula el movimiento de los grandes cuerpos del universo y del átomo más ligero; para tal intelecto nada podría ser incierto y el futuro así como el pasado estarían frente sus ojos."
MODELO DE LAPLACE
Su definición nos dice que:
sea E un experimento cualquiera y S el conjunto finito de sus resultados posibles tal que  , si suponemos que cada resultado es equiprobable (que ninguno tenga más oportunidades que otro), entonces
, si suponemos que cada resultado es equiprobable (que ninguno tenga más oportunidades que otro), entonces 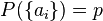 Si queremos que P sea una función de probabilidad tal que
Si queremos que P sea una función de probabilidad tal que 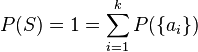 entonces
entonces  .
.
 , si suponemos que cada resultado es equiprobable (que ninguno tenga más oportunidades que otro), entonces
, si suponemos que cada resultado es equiprobable (que ninguno tenga más oportunidades que otro), entonces 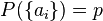 Si queremos que P sea una función de probabilidad tal que
Si queremos que P sea una función de probabilidad tal que 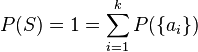 entonces
entonces  .
.
Sea A un subconjunto de S tal que  entonces
entonces
 entonces
entonces 
TRANSFORMACION DE LAPLACE
Aproximadamente en 1744, Euler, seguidor de Lagrange, empezó a buscar una solución para las ecuaciones diferenciales en forma de:
y 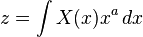
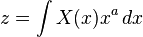
En 1785, Laplace encontró la llave siguiente, utilizando integrales
en forma de transformaciones de ecuaciones diferenciales, que
simplemente era la forma de la solución, y encontró que la ecuación
transformada era fácil de resolver, incluso más que la original.
fuente: Wilkipedia